一次方程式は未知の数を求めるのに便利な方法です。
たとえば小学校の算数で扱ってきた文章題などにおいて図や表でなんとか工夫して答えを導出していた問題でも、一次方程式を使えば一気に簡単になることが多いです。
ただし文字の置き換え方や方程式の立て方など、ポイントをしっかり抑える必要があります。今回は一次方程式の文章問題の解き方について解説していきます。
目次
一次方程式の文章問題のポイント
まず一次方程式の文章題を解く手順を挙げると次の通り。
- 求める値を文字に置き換える
- 等しい関係のものを見つけて一次方程式を立てる
- 一次方程式を解く
では具体的な例で見ていきましょう。
例題
60gのみかん何個かを120gのダンボールに入れたら全体で660gになった。ダンボールに入れたみかんの個数を求めよ。

1.求める値を文字に置き換える

この問題で求める値は“みかんの個数”なので、これを\(x\)個と置きます。
今回の例では未知の値がみかんの数だけなので、そこまで悩まないと思います。
しかし未知の値が問題文に複数出てくることもあるので、「問われているものを文字で置き換える」ということはしっかり抑えておくと良いでしょう。
2.等しい関係のものを見つけて一次方程式を立てる
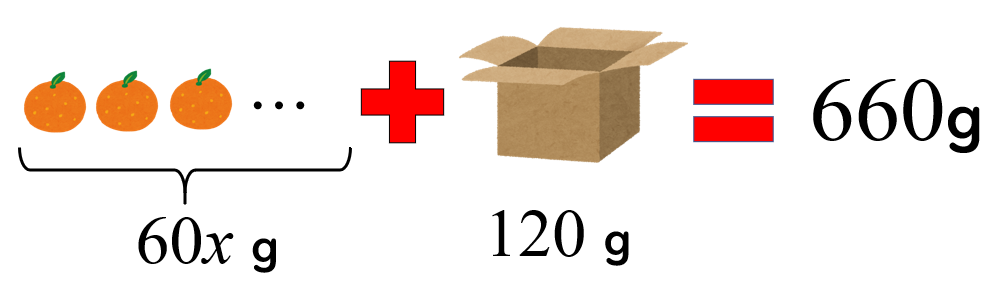
「みかん\(x\)個とダンボールの重さを合わせたら660g」なので、「(みかん\(x\)個の重さ)+(ダンボールの重さ)=660g」という等式を立てることができます。
みかんとダンボールの重さに問題文で与えられた数値を入れると以下の一次方程式になります。
\(60x+120=660\)
3.一次方程式を解く
一次方程式の解き方は前回くわしく解説しました。

等式の性質を利用して「\(x=\)」の形に変形します。丁寧に変形していくと以下の通り。
\(60x+120=660\)
\(60x+120-120=660-120\)
\(60x=540\)
\(60x÷60=540÷60\)
\(x=9\)
\(x\)はみかんの個数を文字に置き換えたものなので、みかんの個数は9個というのが求められました。
基本的にはどのような問題でも以上の手順で説いていきます。さらにいくつかのパターンの問題を見ていきましょう。
一次方程式の文章問題の解き方
問題1(和差算)
Aくんが持っているお金はBくんよりも1200円少なく、さらに2人の所持金を合わせると4400円だった。Aくんの所持金はいくらか。
この問題ではAくんとBくんの両方の所持金が不明ですが、問われているAくんの所持金の方を\(x\)円とします。
問題文は2つの状態について情報が与えられているので、これらからBくんの所持金を表す式を立てます。
- 「Aくんの所持金はBくんよりも1200円少ない」⇒Bくんの所持金:\(x+1200\)
- 「AくんとBくんの所持金を合わせたら4400円」⇒Bくんの所持金:\(4400-x\)
これらを等式で結んで解いたらAくんの所持金を求めることができます。
\(x+1200=4400-x\)
\(x+x=4400-1200\)
\(2x=3200\)
\(x=1600\)
Aくんの所持金は1600円です。
ちなみにこのように複数の未知数の和と差の情報が与えられた文章問題は『和差算』と言い、小学校算数では線分図などを利用して解きます。
問題2(つるかめ算)
1個210円のりんごと1個160円の桃を合計12個買ったら2320円だった。買ったりんごの個数を求めよ。
この問題でもりんごと桃の個数ともに不明ですが、問われているりんごの個数\(x\)個とします。すると桃の数は\((12-x)\)個です。
あとは「りんごの\(x\)個の値段と桃の\((12-x)\)個の値段を合わせたら2320円」という情報を等式で表したら一次方程式になります。
\(210x+160(12-x)=2320\)
\(210x+1920-160x=2320\)
\(50x=2320-1920\)
\(50x=400\)
\(x=8\)
りんごの個数が8個というのが求まりました。
ちなみにこのような文章問題は『つるかめ算』と言い、小学校算数では面積図や図表などを利用して解きます。

問題3(過不足算)
ある人数で居酒屋で食事をした。そのときの代金は、1人2100円ずつ払うと2900円足りず、2500円ずつ払うと500円足りない。食事をした人数を求めよ。
人数と食事の代金はどちらも不明ですが、問われている人数の方をx人と置きましょう。
問題文は2つの状態について情報が与えられているので、これらから食事の代金を表す式を立てます。
- 「1人2100円ずつ払うと2900円足りない」⇒食事の代金:\(2100x+2900\)
- 「1人2500円ずつ払うと500円足りない」⇒食事の代金:\(2500x+500\)
これらを等式で結んで解いたら人数を求めることができます。
\(2100x+2900=2500x+500\)
\(2100x-2500x=500-2900\)
\(-400x=-2400\)
\(x=6\)
人数は6人というのが求まりました。
ちなみにこのような文章問題は『過不足算』と言い、小学校算数では図表などを利用して解きます。

問題4(過不足算)
ある人数で居酒屋で食事をした。そのときの代金は、1人2000円ずつ払うと3100円足りず、2500円ずつ払うと100円足りない。食事の代金を求めよ。
次は食事の代金が問われている場合について考えましょう。食事の代金をx円と置きます。
次は人数に関する式を立てます。
- 「1人2000円ずつ払うと3100円足りない」⇒人数:\(\dfrac{x-3100}{2000}\)
- 「1人2500円ずつ払うと100円足りない」⇒人数:\(\dfrac{x-100}{2500}\)
これらを等式で結んで解いたら代金を求めることができます。
\(\dfrac{x-3100}{2000}=\dfrac{x-100}{2500}\)
分母の最小公倍数10000を両辺にかけます。
\(5(x-3100)=4(x-100)\)
\(5x-15500=4x-400\)
\(x=-400+15500\)
\(x=15100\)
代金が15100円というのが求まりました。
問題5(差集め算)
ケーキがいくつかあり、これらを箱に2個ずつ詰めると、6個ずつ詰めたときよりも4箱多くなる。どちらも過不足なくケーキが詰められる場合、ケーキは全部で何個か。
問われているケーキの個数をx個と置きましょう。
箱の数を考えるとケーキを2個ずつ詰めたら\(\dfrac{x}{2}\)箱、6個ずつ詰めたら\(\dfrac{x}{6}\)箱となります。
そして2個ずつ詰めたら6個ずつ詰めた時よりも4箱多くなるので、これを方程式に表して解くと以下の通り。
\(\dfrac{x}{2}-\dfrac{x}{6}=4\)
\(3x-x=24\)
\(2x=24\)
\(x=12\)
ケーキの数が12個というのが求まりました。
ちなみにこのような文章問題は『差集め算』と言い、小学校算数では図表や面積図などを利用して解きます。
問題6(差集め算)
1冊の問題集を1日10問ずつ解いていくと、1日5問ずつ解いていくよりも5日早く終わらせることができる。問題集は全部で何問か。
問われている問題の数をx問と置きましょう。
問題を解き終わる日数について考えると1日10問ずつ解いたら\(\dfrac{x}{10}\)日、5問ずつ解いたら\(\dfrac{x}{5}\)日となります。
そして10問ずつ解いたら5問ずつ解くよりも5日早く終わるので、これを方程式に表して解くと以下の通り。
\(\dfrac{x}{5}-\dfrac{x}{10}=5\)
\(2x-x=50\)
\(x=50\)
問題の数が50問というのが求まりました。
ちなみにこちらの問題も差集め算なので、小学校算数では図表や面積図を用いて解く問題です。
練習問題
一次方程式の文章問題を練習できるものを用意しました。下の「スタート」を押して問題の答えを入力したら「答え合わせ」押してください。
回答の正解・不正解や問題の計算過程などが表示されます。
また、暗算では難しいので何か書けるものを用意してから取り組むのをおすすめします。
00:00
一次方程式の文章問題についていろいろと見てきましたが、小学校算数では複雑だった問題でも方程式を使うことで簡単に解くことができるのが分かるかと思います。
ただし与えられた情報から一次方程式を立てるには、しっかりポイントを抑えてある程度問題をこなすのが必要になります。
そこで自由に印刷できる一次方程式の文章問題集も用意しました。数値はランダムで変わり無数に問題を作ることができるので、ぜひご活用ください。