小数の掛け算の計算手順｜小学生に分かりやすく教える方法

整数の掛け算ができるようになれば、つぎは小数の掛け算へとステップアップしますが、小数点を含む問題はイメージしにくいのでつまづく子も多いです。

大人でも小数点の計算を感じている人は多いのではないでしょうか？

しかし実際はあるポイントさえ押さえていれば、あとは整数の掛け算と全く同じように解くことができるのです。

今回は小数の掛け算を小学生に分かりやすく教える際のポイントを解説していきます。

小数の掛け算の手順

小数の掛け算の手順としては以下の通り。

たとえば$2.52×3.1$の場合。

小数点を無視して整数として計算すると、
$252×31＝7812$

小数点以下の数字の個数は計$3$つなので、$7812$の小数点を$3$桁移動させて$7.812$となる。

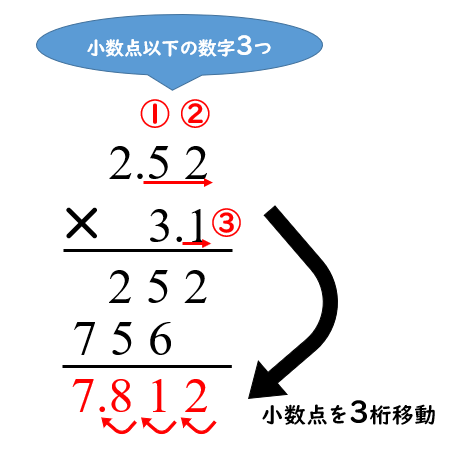
小数点の処理はこれだけで解決するので、実質整数の掛け算とたいして違いはありません。

もちろん小数点処理の問題以前に、整数の掛け算がきちんと習得できていないと絶対に解けないので、ここがあやふやの場合はまずはこちらを理解しましょう。

また小数点の処理はこれを丸暗記するのではなく、「なぜこの方法で小数点が計算できるのか」というのを理解するのが重要です。

小数の掛け算の仕組みとしては、厳密には以下のように計算しています。

$$2.52×3.1＝（2.52×100×0.01）×（3.1×10×0.1）＝252×31×0.01×0.1＝7812×0.001＝7.812$$

整数として処理するためにはじめに$100$倍や$1000$倍などをして、整数の計算が終わった後にはじめにかけた分の数字を割るのです。

法則を用いなくても直感的に理解できるかもしれませんが、これは「掛け算の順番を入れ替えても答えが変わらない」という交換法則を用いた手法です。

わざわざ『交換法則』という言葉を使うと逆にこんがらがる子もいると思うので、「最初に$100$や$1000$などをかけて整数にして、後からかけた分の数字で割るんだよ」という風に教えた方がいいかもしれません。

小数の掛け算の手順は丸暗記でもそこまで困らないかもしれませんが、いざ本番ど忘れしたときでも困らないように、きちんと仕組みを理解するのが大事です。

お子さんに教える際にはぜひ参考にしてください。

ちなみに、小数の掛け算の計算ドリルは自由に印刷できるものを用意しています。ぜひご活用ください。