中学受験では「速さ」に関していろんな文章問題が出題されますが、そのひとつとして『通過算』が挙げられます。
通常の速さの問題は、幅を無視できる人やものが一定の距離を移動する際の時間や速さなどが問われます。
これに対し、通過算は動くものが幅を持ち、それを考慮しないといけないので少し複雑です。
ただし通過算は出題されるパターンはほぼ定形なので、慣れてしまえばそこまで怖い問題ではありません。
今回は通過算の基本から応用問題までわかりやすく図で解説していきます。
通過算とは
通過算とは電車や新幹線などの幅をもったものが何かを完全に通過する際の速さや時間などを求める問題です。
たとえばこのような問題。
例題1
全長600mの電車が1000mのトンネルに入りはじめてから出終わるまで40秒かかった。電車の速さは時速何kmか。

人が移動するのとは違い、移動する物体の幅が問題に関係してきます。
他には動いているもの同士がすれ違う問題。
例題2
長さ350mで秒速11mで走る電車Aと長さ217mで秒速16mの電車Bが出会ってからすれ違うのに何秒かかるか。

動いているものを追い越す問題。
例題3
長さ350mで秒速58mで走る電車Aが長さ772mで秒速25mの電車Bを追いついてから追い抜くのにかかる時間は何秒後か。

これら3つが通過算の代表的なパターンです。
- 止まっているものを動いているものが通過する
- 動いているもの同士がすれ違う
- 動いているものが動いているものを追い越す
ではこれらをどのようにして解くのか、解説していきます。
通過算の解き方
例題1(止まっているものを通過)
例題1
全長600mの電車が1000mのトンネルに入りはじめてから出終わるまで40秒かかった。電車の速さは時速何kmか。

幅を持たない人などがトンネルを通過する場合であれば、40秒で1000m移動したので時速1000÷40=25mになります。
しかしこの問題では600mの幅を持つ電車がトンネルを入り始めてから出終わるまでなので、40秒で「トンネルの長さ」に「車両の長さ」を加えた距離だけ移動したことになるのです。
下のような図を書いて、車両の先頭がどれだけ移動したかを考えれば分かりやすいと思います。

40秒で1600m移動したので、速さは1600÷40=40より、秒速40m。
これを時速にしてkmに換算します。
1分=60秒、1時間=60分=3600秒、1m=0.001kmなので、
40×3600÷1000=40×3.6=144
秒速40mは時速144kmとなります。答えは時速144kmです。
例題2(動いているもの同士がすれ違う)
例題2
長さ350mで秒速11mで走る電車Aと長さ217mで秒速16mの電車Bが出会ってからすれ違うのに何秒かかるか。

それぞれの電車の先頭が揃ってから最後尾が揃うまでの時間を求めます。
すれ違う問題では「移動距離の和=車両の長さの和」となるのがポイントです。
AとBが移動した距離をあわせたら車両の長さの和(567m)になります。そして1秒で進む距離の和(速度の和)は27mなので、567÷27=21。
答えは21秒です。
例題3(動いているものを追い越す)
例題3
長さ350mで秒速58mで走る電車Aが長さ772mで秒速25mの電車Bを追いついてから追い抜くのにかかる時間は何秒後か。
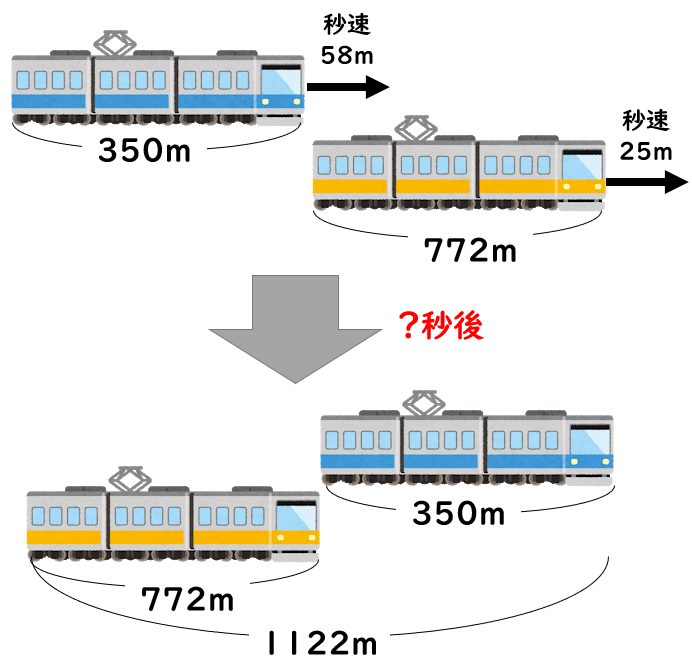
Aの先頭とBの最後尾が揃ってからAの最後尾とBの先頭が揃うまでの時間を求めます。
追い越す問題では「移動距離の差=車両の長さの和」となるのがポイントです。
AがBよりも1122m長い距離を移動するまでの時間を求めればいいわけです。
そして1秒で進む距離の差は速度の差になるので、58-25=33より、1秒でAがBよりも33m長い距離を移動します。
1122÷33=34より、答えは34秒です。
通過算は以上の3つが主なパターンです。問われていることをしっかり把握するためにも、図を書いて考えるのが重要になります。
通過算の応用問題
さらに通過算の応用問題について見ていきましょう。和差算との複合問題です。
通過算の応用問題
長さ300mの電車Aと長さ350mの電車Bが出会ってすれ違うまで10秒、電車Aが電車Bに追いついてから追い抜くのに130秒かかった。電車Aと電車Bの速さはそれぞれ秒速何mか。
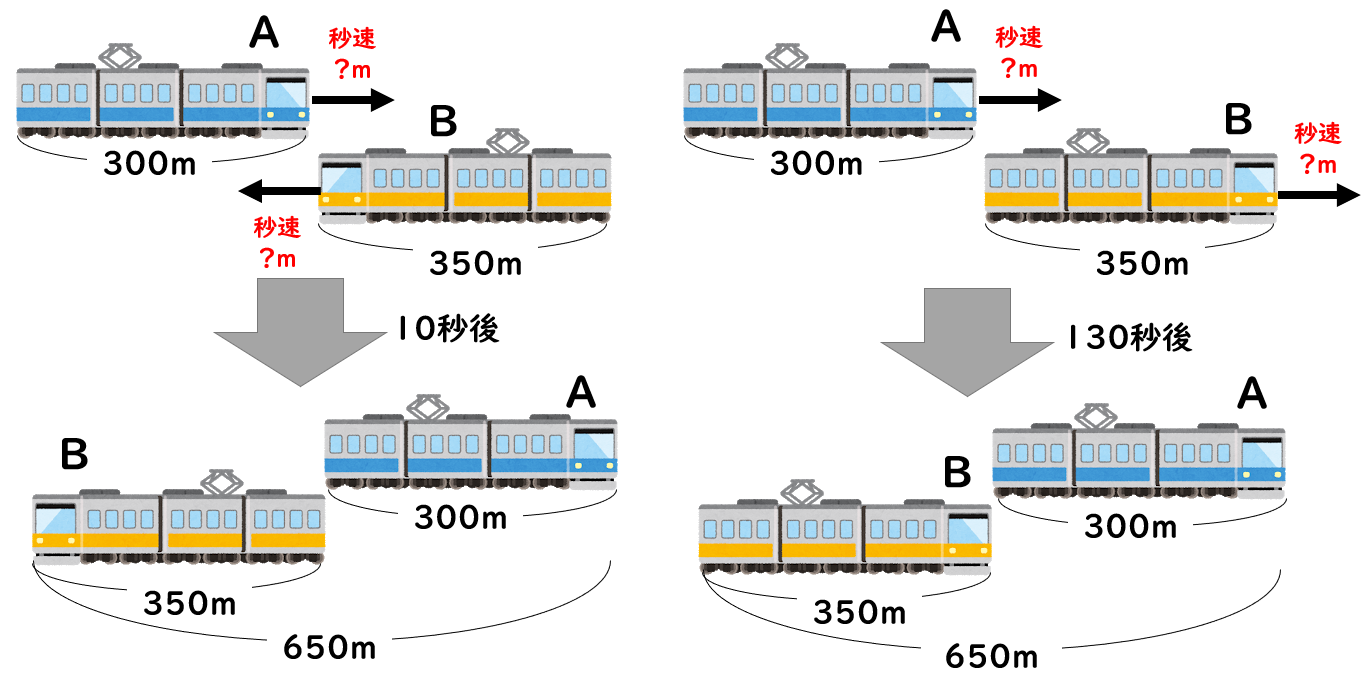
例題でも述べましたが、すれ違う場合は「移動距離の和=車両の長さの和」となり、追い越す問題では「移動距離の差=車両の長さの和」となるのがポイントです。
すれ違う場合について考えると、AとBの10秒間の移動距離が650mなので、650÷10=65より1秒で65m。
つまり、『Aの秒速+Bの秒速=65m』
追い抜く場合について考えると、130秒間でAがBよりも650m長い距離を移動したということなので、650÷130=5より1秒で5m。
つまり、『Aの秒速-Bの秒速=5m』
2つの不明な値の和と差が分かれば、これらを足して2で割ったら大きな方の値、引いて2で割ったら小さな方の値になります。
和差算の解き方ですが、数直線を書いたら理解しやすいでしょう。
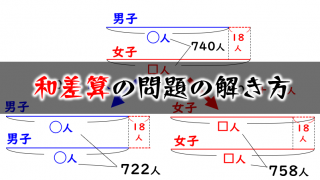

「AとBの和の65」と「AとBの差の5」を足したらAの2倍の値になり、逆に引いたらBの2倍の値になります。
なのでそれぞれの秒速は以下の通り。
Aの秒速=(65+5)÷2=35(m)
Bの秒速=(65-5)÷2=30(m)
答えはA:秒速35m、B:秒速30mです。
応用問題でも、もとは通過算の3つのパターンのどれかが根底にあるので、それぞれのパターンについて慣れるのが大事です。
通過算に限らず、文章問題では図を書いて状況を把握するのが大事なので、図を書く癖をつけましょう。
ちなみに通過算について、自由に印刷できる練習問題を用意しました。数値はランダムで変わり無数に問題を作ることができるので、ぜひご活用ください。











よくわかりました!ありがとうございます!