図形を拡大・縮小したものを相似といいますが、三角形の場合、相似であることを証明するための条件があります。合同と同様です。
今回は三角形の相似条件や三角形の相似を証明する問題の解き方について見ていきましょう。
相似な図形とは?
2つの図形において、「片方がもう一方に対して、拡大または縮小した図形になっている場合、その関係」を相似といい、∽という記号で表します。
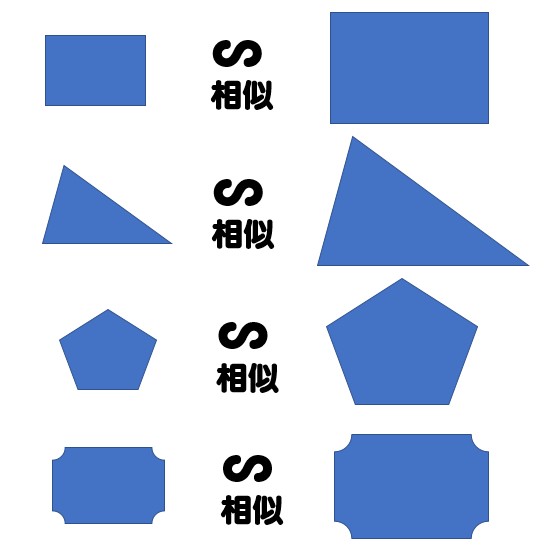
多角形の場合、角の大きさは全て一致しますが、辺の長さは同じ比率だけ異なります。
また、相似な図形の大きさの比率を“相似比”といいます。
そして対応する各辺の長さの比は相似比と等しいです。
下の図は相似な関係にある四角形ですが、それぞれの対応する辺が相似比と等しい1:2になっているのが確認できるかと思います。

合同の場合は形だけでなく大きさも同じ図形を指しましたが、それに対し相似とは形だけが同じで大きさが異なる図形を指します。
- 合同な図形:形も大きさも同じ図形
- 相似な図形:形は同じで大きさが異なる図形
三角形の相似条件とは?
まず三角形の合同条件について復習しましょう。
以下の3つの条件のうち、どれか一つでも確認できれば2つの三角形が合同であるといえます。
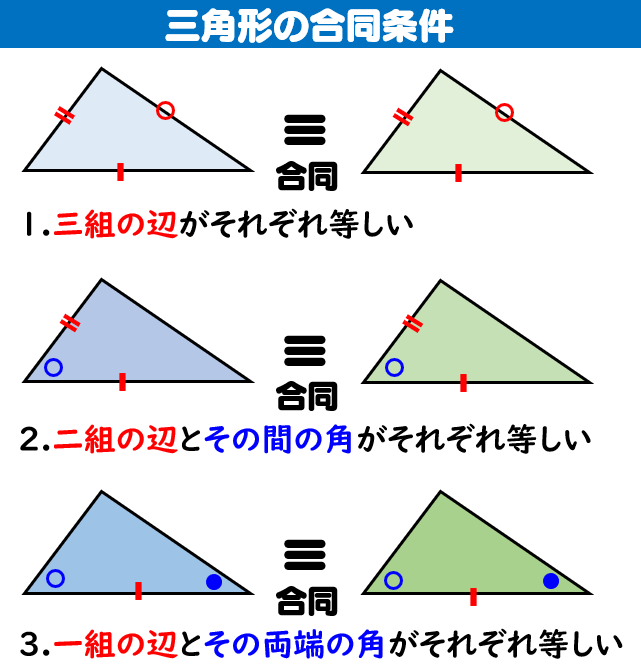

これと同じように、三角形が相似であることを確認するための条件があります。
- 3組の辺の比がそれぞれ等しい
- 2組の辺の比とその間の角がそれぞれ等しい
- 2組の角がそれぞれ等しい

合同条件と似ているのがわかるかと思います。
1番目と2番目は「辺」が「辺の比」になり、3番目は「辺の長さに関する条件」がなくなったものです。
ではこの三角形の相似条件をどのように使うのか、実際に問題を解きながら見ていきましょう。
三角形の相似の証明問題
例題
次の図において、2つの三角形が相似であることを証明せよ。

△ABOと△DCOにおいて、
対頂角より、∠AOB=∠DOC・・・①
AO:DO=BO:CO=2:3・・・②
①②より、2組の辺とその間の角が等しいので、
△ABO∽△DCO
証明問題のポイント
以上の解答は合同の証明問題と同様、決まった形式なので必ず抑えましょう。
- 証明条件の要素をひとつずつ挙げていく
- 「〇〇なので、〇〇・・・①」
- 「〇〇なので、〇〇・・・②」
- どの合同条件を満たすのかを書いて結論につなげる
- 「①②より(相似条件)なので△○○○∽△○○○」
辺の比が等しいことを示すのは少しややこしく感じるかもしれませんが、証明の流れは合同の証明と同じです。
パターンもだいたい決まっているので、慣れてしまえば難しくはありません。





